¿Que es una figura geométrica?
Una figura geométrica corresponde a un espacio encerrado entre lineas
Las figuras geométricas de lados rectos se denominan polígonos y las figuras de lados se denominan circulo y circunferencia y también corresponden a polígonos
Elementos de un polígono:
- Vértice: Es el punto de intersección de dos segmentos contiguos. Se designa con letras mayúsculas A, B, C, D ...
- Lado: Es un fragmento de recta que esta comprendido entre 2 vértices. Se designa con dos letras mayúsculas ubicadas en sus extremos, o con una letra minúscula en correspondencia con el vértice opuesto: AB = d, BC= e, CD = a, DE= b, EA= c.
- Ángulo interior: Es un ángulo formado por dos lados del polígono. Un ángulo interior se designa con una letra griega o con las tres letras mayúsculas de los vértices que le correspondan.
- Ángulo exterior: Es el ángulo formado por un lado del polígono y la prolongacion de otro contiguo hacia la región exterior
- Diagonal: Es un segmento de recta que une un vértice interior de un polígono con el vértice no consecutivo a el
Clasificación de los polígonos:
- Según el numero de lados que poseen:
1) Triángulo: Es un polígono de tres lados.
Elementos de un triángulo:
Un triángulo esta formado por 3 ángulos interiores, 3 ángulos exteriores, 3 lados y 3 vértices.
Propiedades:
- La suma de sus ángulos interiores siempre da 180°.
- La suma de sus ángulos exteriores siempre da 360°.
- La suma de las longitudes de dos de sus lados es siempre mayor que la longitud del tercer lado.
Clasificación de los triángulos:
Según la medida de sus lados:
- Equilatero: Tiene sus 3 lados de igual medida y sus 3 ángulos de igual medida (cada uno de 60°).
- Isosceles: Tiene 2 de sus lados de igual medida, y por lo tanto, 2 ángulos de igual medida.
- Escaleno: Tiene todos sus lados y ángulos de diferente medida.
Según la medida de sus ángulos:
- Acutangulo: Tiene sus 3 ángulos agudos, es decir, sus ángulos miden menos de 90°.
- Rectángulo: Tiene 1 ángulo recto, es decir, uno de sus ángulos mide 90°.
- Obtusangulo: Tiene un ángulo obtuso, es decir, uno de sus ángulos mide mas de 90° y menos de 180°.
2) Cuadriláteros: Polígono de 4 lados
Elementos de un cuadrilátero:
- 4 vértice
- 4 lados
- 4 ángulos exteriores
- 4 ángulos interiores
- 2 diagonales
Propiedades:
- La suma de sus ángulos interiores siempre da 360°
- La suma de sus ángulos exteriores siempre de 360°
Clasificacion de los cuadriláteros:
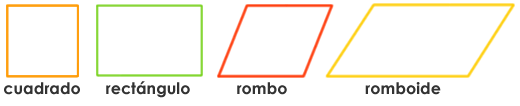
- Pararelogramos: Son aquellos cuadriláteros que tienen dos pares de lados pararelos. Los paralelogramos son: el cuadrado, el rectángulo, el rombo y el romboide
a) Cuadrado: Todos sus lados son de igual medida. Posee 4 ángulos rectos
b) Rectángulos: Posee 2 pares de lados de igual medida. Tiene 4 ángulos rectos
c) Rombo: Todos sus lados son de igual medida. Posee 2 ángulos agudos y 2 ángulos obtusos.
d) Romboide: Posee 2 pares de lados de igual medida. Tiene 2 ángulos agudos y 2 obtusos
- Trapecios: Son aquellos cuadriláteros que poseen solamente un par de lados paralelos. Existen cuatro tipos de trapecios
a) Trapecio isosceles: Posee un par de lados pararelos de igual medida
b) Trapecio trisolatero: Es aquel que tiene 3 lados de igual medida
c) Trapecio rectángulo: Es aquel que tiene 2 ángulos rectos
d) Trapecio escaleno: Todos sus lados son de distinta medida
- Trapezoides: Son aquellos cuadriláteros que no poseen lados paralelos. Existen 2 tipos
a) Trapezoide simétrico: Tiene 2 pares de lados de igual medida
b) Trapezoide asimétrico: Puede tener 2, 3 o bien ningún lado de igual medida
Circulo y circunferencia
Circulo: Es una figura plana delimitada por una circunferencia

Circunferencia: Es el conjuno de todos los puntos del plano que equidistan de un mismo punto llamado centro de la circunferencia
Elementos de una circunferencia:
a) Radio: Es un segmento que une el centro del circulo con cualquier punto de la circunferencia. La medida del radio es constante
b) Cuerda: Es el segmento que une dos puntos de la circunferencia. Las cuerdas tienen distintas medidas
c) Diametro: Es la cuerda que pasa por el centro de la circunferencia. El diametro es la cuerda de mayor medida. El diametro es el doble del radio
d) Tangente: Es la recta que intersecta solo un punto de la recta
e) Arco: Es la parte de la circunferencia que comprende dos puntos de ella
f) Segmento Circular: Es cada una de las partes en que se divide un circulo cuando se traza una cuerda. Si la cuerda es un diametro, cada parte sera un semicirculo
g) Sector Circular: Es la parte del circulo limitada por dos radios y un arco




















.jpg)










.jpg)